Sub-Chapter 11.11

 

11.11 DESIGNING COUNTERS WITH ARBITRARY SEQUENCES

 

[KEMBALI KE MENU SEBELUMNYA]

DAFTAR ISI

1. Tujuan

2. Alat dan Bahan

3. Dasar Teori

4. Percobaan

5. Video

6. Example

7. Problem

8. Pilihan Ganda

9. Link Download

1. Tujuan [kembali] 

    

• Mengetahui apa itu adder subtractor.

• Memahami prinsip kerja adder subtractor.

• Dapat merangkai rangkaian adder subtractor

2. Alat dan Bahan [kembali] 

A. Alat

     1.     Power Supply

        Power Supply atau dalam bahasa Indonesia disebut dengan Catu Daya adalah suatu alat listrik             yang dapat menyediakan energi listrik untuk perangkat listrik ataupun elektronika lainnya.

    2.     Voltmeter DC

    Difungsikan guna mengukur besarnya tegangan listrik yang terdapat dalam suatu rangkaian listrik. Dimana, untuk penyusunannya dilakukan secara paralel sesuai pada lokasi komponen yang sedang diukur.

3.     Generator DC

 

4.     logicprobe

    Logic probe atau logic tester adalah alat yang biasa digunakan untuk menganalisa dan mengecek status logika (High atau Low) yang keluar dari rangkaian digital. Objek yang diukur oleh logic probe ini adalah tegangan oleh karena itu biasanya rangkaian logic probe harus menggunakan tegangan luar (bukan dari rangkaian logika yang ingin diukur) seperti baterai. Alat ini biasa digunakan pada IC TTL ataupun CMOS (Complementary metal-oxide semiconductor).

    Logic probe menggunakan dua lampu indikator led yang berbeda warna untuk membedakan keluaran High atau Low. Yang umum dipakai yaitu LED warna merah untuk menandakan output berlogika HIGH (1) dan warna hijau untuk menandakan output berlogika LOW(0).

 

5.     Baterai (12 V)

Merupakan penyuplai energi berupa listrik.

          B. Bahan

    1.     Logicstate 

 

Logicstate berfungsi untuk memberi tegangan rendah atau tinggi, atau logika 1 atau logika 0.

 

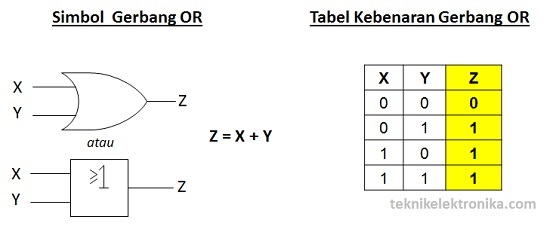
    2.     Gerbang Logika OR

    Gerbang OR memerlukan 2 atau lebih Masukan (Input) untuk menghasilkan hanya 1 Keluaran (Output). Gerbang OR akan menghasilkan Keluaran (Output) 1 jika salah satu dari Masukan (Input) bernilai Logika 1 dan jika ingin menghasilkan Keluaran (Output) Logika 0, maka semua Masukan (Input) harus bernilai Logika 0. Simbol yang menandakan Operasi Logika OR adalah tanda Plus (“+”). Contohnya : Z = X + Y.

Simbol dan Tabel Kebenaran Gerbang OR (OR Gate) :

 

Gerbang Logika OR (IC 7432)

    Gerbang OR atau disebut juga "OR GATE" adalah jenis gerbang logika yang memiliki dua input (Masukan) dan satu output (keluaran). Meskipun memiliki pengertian yang sama dengan gerbang OR tapi memiliki perbedaan pada simbol dan tabel kebenaran.

Konfigurasi pin IC 7432:

    3.     Gerbang AND

        

Konfigurasi:

Spesifikasi : 

Supply Voltage 7V Input Voltage 5.5V Operating Free Air Temperature 0°C to +70°C Storage Temperature Range -65°C to +150°C

    4.     Gerbang Logika XOR

 

Gerbang logika XOR adalah singkatan dari EXclusive OR gate yang outputnya hanya akan bernilai logika 1 jika salah satu input X atau Y dalam keadaan bernilai logika 1, ketika semua inputnya dalam keadaan logika 0 atau dalam keadaan logika 1 maka output akan tetap logika 0.

  3. Dasar Teori [kembali] 

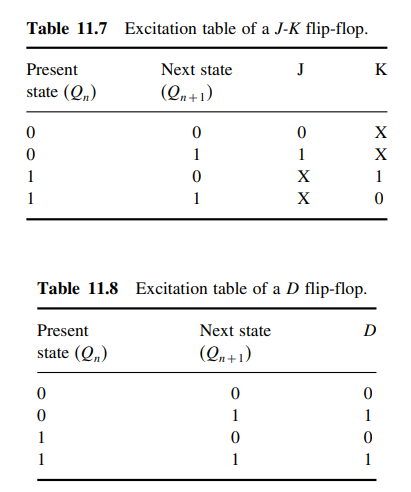
    Tabel eksitasi mirip dengan tabel karakteristik yang kita bahas di bab sebelumnya tentang sandal jepit. Tabel eksitasi mencantumkan keadaan sekarang, keadaan berikutnya yang diinginkan dan input flip-flop (J, K, D, dll.) yang diperlukan untuk mencapai itu. Hal yang sama untuk flip-flop JK dan flip-flop D ditunjukkan pada Tabel 11.7 dan 11.8 masing-masing. Mengacu pada Tabel 11.7, jika output dalam keadaan logika '0' dan diinginkan bahwa ia pergi ke keadaan logika '1' pada terjadinya pulsa clock, input J harus dalam keadaan logika '1' dan input K dapat berada dalam keadaan logika '0' atau logika '1'. Ini benar karena, untuk transisi '0' ke '1', ada dua kemungkinan kondisi input yang dapat mencapai hal ini. Ini adalah J = 1, K = 0 (mode SET) dan J = K = 1 (mode sakelar), yang selanjutnya mengarah ke J = 1 K = X (baik 0 atau 1). Entri lain dari tabel eksitasi dapat dijelaskan pada baris yang sama. Dalam kasus flip-flop D, input D sama dengan status logika dari keadaan berikutnya yang diinginkan. Ini benar karena, dalam kasus flip-flop D, input D ditransfer ke output pada terjadinya pulsa clock, terlepas dari status logika output Q saat ini.

Diagram Transisi Keadaan
 
    Diagram transisi keadaan adalah representasi grafis dari berbagai keadaan dari rangkaian sekuensial tertentu dan urutan terjadinya keadaan-keadaan ini sebagai respons terhadap masukan jam. Negara bagian yang berbeda diwakili oleh lingkaran, dan panah yang menghubungkannya menunjukkan urutan terjadinya negara bagian yang berbeda. Sebagai contoh, Gambar 11.24 menunjukkan diagram transisi keadaan dari pencacah biner MOD-8.
 
Prosedur Desain
 
    Kami akan mengilustrasikan prosedur desain dengan bantuan sebuah contoh. Kami akan melakukan ini untuk desain pencacah sinkron MOD-6, yang mengikuti urutan penghitungan 000, 010, 011, 001, 100, 110, 000, 010, : 

1. Tentukan jumlah sandal jepit yang diperlukan untuk tujuan tersebut. Identifikasi keadaan yang tidak diinginkan. Dalam
kasus ini, jumlah flip-flop yang diperlukan adalah 3 dan keadaan yang tidak diinginkan adalah 101 dan 111
2. Gambarlah diagram transisi keadaan yang menunjukkan semua keadaan yang mungkin terjadi termasuk keadaan yang tidak diinginkan.
Negara bagian yang tidak diinginkan harus digambarkan sedang transit ke negara bagian mana pun yang diinginkan. Kami telah memilih
negara bagian 000 untuk tujuan ini. Penting untuk menyertakan keadaan yang tidak diinginkan untuk memastikan bahwa, jika penghitung
secara tidak sengaja masuk ke salah satu keadaan yang tidak diinginkan ini karena kebisingan atau peningkatan daya, penghitung akan
menuju ke keadaan yang diinginkan untuk melanjutkan urutan yang benar pada penerapan jam berikutnya. detak. Gambar 11.25
menunjukkan diagram transisi keadaan

3. Gambarkan tabel eksitasi untuk pencacah, daftarkan keadaan saat ini, keadaan selanjutnya yang sesuai dengan keadaan sekarang dan status logika yang diperlukan dari masukan flip-flop (JDanKmasukan jika penghitung ingin diimplementasikanJKsandal jepit). Tabel eksitasi ditunjukkan pada Tabel 11.9

Tabel eksitasi rangkaian dapat digambarkan dengan sangat mudah setelah kita mengetahui tabel
eksitasi dari flip-flop yang akan digunakan untuk membangun counter. Misalnya, mari kita lihat baris
pertama tabel eksitasi (Tabel 11.9). Pencacah berada dalam keadaan 000 dan akan menuju ke 010 jika diterapkan pulsa jam. Artinya, keluaran normal dariC, BDanAsandal jepit masing-masing harus
menjalani transisi '0' ke '0', '0' ke '1' dan '0' ke '0'. Mengacu pada tabel eksitasi aJKflip-flop, transisi yang diinginkan dapat terwujud jika status logikanyaJA,KA,JB,KB,JCDanKCseperti yang ditunjukkan pada tabel eksitasi.
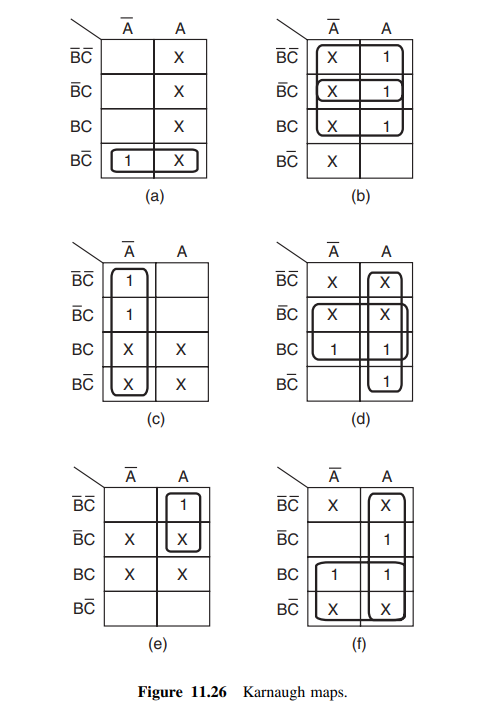
4. Langkah selanjutnya adalah merancang rangkaian logika untuk pembangkitanJA,KA,JB,KB,JCDanKCmasukan dari yang tersediaA, A, B, B, CDanCkeluaran. Hal ini dapat dilakukan dengan menggambar peta Karnaugh untuk setiap masukan, meminimalkannya, dan kemudian menerapkan ekspresi Boolean yang diperkecil. Peta Karnaugh untuk JA,KA,JB,KB,JCDan KC masing-masing ditunjukkan pada Gambar 11.26(a), (b), (c), (d), (e) dan (f).
Ekspresi Boolean yang diperkecil adalah sebagai berikut:

Ekspresi di atas sekarang dapat digunakan untuk mengimplementasikan rangkaian kombinasional untuk menghasilkanJA,KA, JB,KB,JCDanKCmasukan. Gambar 11.27 menunjukkan rangkaian counter lengkap.

4. Percobaan [kembali] 

• Figure 11.27

• Figure 11.29

Analisis Rangkaian Counter

Gambar yang diberikan menunjukkan rangkaian counter yang terdiri dari tiga flip-flop (FF-A, FF-B, dan FF-C) serta beberapa gerbang logika yang saling terhubung. Untuk memahami fungsionalitas rangkaian ini, mari kita analisis koneksi dan menentukan urutan penghitung serta perilaku keseluruhannya.

Analisis Rangkaian

1. Flip-Flop dan Input:

2. Gerbang Logika:
• Ada tiga gerbang AND dan satu gerbang OR.
3. Koneksi:
• Sinyal clock terhubung ke ketiga flip-flop, menunjukkan operasi sinkron.
• Output dari FF-A (A) digunakan sebagai input ke gerbang AND yang terhubung ke FF-B.
• Output dari FF-B (B) digunakan sebagai input ke gerbang AND yang terhubung ke FF-C.
• Output dari gerbang AND digabungkan dalam gerbang OR untuk menghasilkan kondisi berikutnya untuk FF-C.
• Kombinasi dari output flip-flop dan gerbang logika menentukan perilaku keseluruhan rangkaian.

Fungsionalitas dan Urutan Penghitung

Untuk menentukan urutan penghitung, kita perlu mengamati perubahan keadaan flip-flop berdasarkan logika yang diimplementasikan. Mari kita evaluasi perubahan keadaan langkah demi langkah untuk setiap pulsa clock:

1. Keadaan Awal: Anggap keadaan awal dari flip-flop adalah (A,B,C)=(0,0,0)(A, B, C) = (0, 0, 0)(A,B,C)=(0,0,0).
2. Logika Transisi Keadaan:
• Transisi keadaan akan bergantung pada keadaan saat ini dan output dari gerbang logika.
• Setiap flip-flop akan mengubah keadaannya berdasarkan input dari tahap sebelumnya dan output dari gerbang logika.
3. Mengamati Transisi Keadaan: Mari kita analisis kemungkinan transisi dengan mengevaluasi kondisi input untuk setiap flip-flop pada setiap pulsa clock.

Analisis Transisi Keadaan yang Detil

Mengingat sifat sinkron dari flip-flop, kita akan mempertimbangkan input ke setiap flip-flop pada tepi naik dari setiap pulsa clock. Transisi keadaan dapat diuraikan sebagai berikut:

1. FF-A:
• FF-A beralih setiap pulsa clock.
2. FF-B:
• FF-B beralih ketika A dalam keadaan tinggi.
3. FF-C:
• FF-C beralih ketika A dan B keduanya dalam keadaan tinggi (output dari gerbang AND pertama adalah tinggi).

Berdasarkan kondisi-kondisi ini, urutan penghitung mengikuti pola berdasarkan keadaan A, B, dan C.

Urutan Penghitung yang Diharapkan

Berdasarkan operasi umum dari penghitung sinkron dan logika yang disediakan dalam rangkaian, kita dapat menyimpulkan urutan penghitungnya:

1. Mulai dari (A,B,C)=(0,0,0)(A, B, C) = (0, 0, 0)(A,B,C)=(0,0,0).
2. FF-A beralih setiap pulsa clock: AAA = 0, 1, 0, 1, ...
3. FF-B beralih ketika A dalam keadaan tinggi: BBB = 0, 0, 1, 1, 0, 0, 1, 1, ...
4. FF-C beralih ketika A dan B keduanya dalam keadaan tinggi: CCC = 0, 0, 0, 0, 1, 1, 1, 1, ...

Menggabungkan perubahan ini menghasilkan urutan berikut:

• (A,B,C)={(0,0,0),(1,0,0),(0,1,0),(1,1,0),(0,0,1),(1,0,1),(0,1,1),(1,1,1)}(A, B, C) = \{(0, 0, 0), (1, 0, 0), (0, 1, 0), (1, 1, 0), (0, 0, 1), (1, 0, 1), (0, 1, 1), (1, 1, 1)\}(A,B,C)={(0,0,0),(1,0,0),(0,1,0),(1,1,0),(0,0,1),(1,0,1),(0,1,1),(1,1,1)}

Urutan ini menunjukkan bahwa counter menghitung dari 0 hingga 7 dalam biner (penghitung mod-8). 

Kesimpulan

Rangkaian dalam Gambar 11.29 berfungsi sebagai penghitung biner 3-bit, menghitung dari 0 hingga 7 dalam biner. Setiap flip-flop beralih berdasarkan clock dan kondisi output yang didefinisikan oleh gerbang logika. Urutannya berulang setelah mencapai hitungan maksimum 7, menjadikannya sebagai penghitung siklik.

• Figure 11.31

Rangkaian yang ditunjukkan pada gambar adalah sebuah counter (pencacah) berbasis JK flip-flop yang terdiri dari tiga flip-flop (FF-A, FF-B, dan FF-C) yang terhubung dengan beberapa gerbang logika AND dan OR.

Mari kita jelaskan komponen dan koneksi rangkaian ini:

1. Flip-Flop A (FF-A):

§  Masukan J_A dan K_A diatur ke '1' tetap, artinya FF-A akan selalu toggle (berubah keadaan) setiap kali ada sinyal clock.

§  Keluaran A terhubung ke gerbang AND.

2. Flip-Flop B (FF-B):

§  Masukan J_B diatur untuk menerima keluaran dari gerbang AND yang menggabungkan sinyal dari A dan B.

§  Masukan K_B diatur ke '1' tetap, artinya FF-B akan toggle ketika J_B = 1 dan ada sinyal clock.

3. Flip-Flop C (FF-C):

§  Masukan J_C diatur untuk menerima keluaran dari gerbang AND yang menggabungkan sinyal dari A, B, dan C.

§  Masukan K_C diatur ke sinyal terbalik dari C, artinya FF-C akan toggle ketika J_C = 1 dan ada sinyal clock.

4. Gerbang Logika:

§  Beberapa gerbang AND dan OR digunakan untuk menggabungkan keluaran dari flip-flop dan membentuk masukan untuk flip-flop yang lain.

 

Tabel Kebenaran

Untuk membuat tabel kebenaran, kita perlu melihat bagaimana setiap flip-flop berubah berdasarkan keadaan sebelumnya. Asumsikan bahwa A, B, dan C adalah output dari masing-masing flip-flop dan mereka berubah sesuai dengan sinyal clock. Mari kita buat tabel kebenaran berdasarkan kondisi awal 000 (A=0, B=0, C=0):

Penjelasan

·       Flip-Flop A (FF-A): Selalu toggle pada setiap sinyal clock karena J_A dan K_A diatur ke '1'.

·       Flip-Flop B (FF-B): Toggle ketika A = 1 dan B = 0 (berdasarkan gerbang AND masukan J_B).

·       Flip-Flop C (FF-C): Toggle ketika A = 1, B = 1, dan C = 0 (berdasarkan gerbang AND masukan J_C).

Tabel kebenaran menunjukkan bagaimana keluaran A, B, dan C berubah seiring dengan sinyal clock. Setiap kolom clock menunjukkan keadaan A, B, dan C setelah menerima sinyal clock

5. Video [kembali] 

            

        

  6. Example [kembali] 

• Figure 11.27

Tabel 11.10 memberikan tabel eksitasi dari flip-flop tertentu yang mempunyai X1 dan X2 sebagai inputnya. Gambarlah tabel eksitasi rangkaian pencacah sinkron MOD-5 menggunakan flip-flop ini untuk urutan pencacahannya 000, 001, 011, 101, 110, 000, Jika kondisi saat ini tidak diinginkan, maka harus transit ke 110 pada penerapan pulsa jam. Rancang rangkaian counter dengan menggunakan flip-flop yang rangkaian eksitasinya diberikan pada Tabel 11.10

 

solusi 

• Tabel eksitasi rangkaian ditunjukkan pada Tabel 11.11.
• Jumlah sandal jepit yang dibutuhkan adalah 3 buah.
• X1 (A) dan X2 (A) merupakan input dari flip-flop A, yang juga merupakan flip-flop LSB.
• X1 (B) dan X2 (B) mewakili input ke flip-flop B.
• X1 (C) dan X2 (C) adalah masukan ke flip-flop C, yang juga merupakan flip-flop MSB.
• Langkah selanjutnya adalah menggambar peta Karnaugh, masing-masing untuk input berbeda ke tiga flip-flop.
• Gambar 11.28(a) sampai (f) menunjukkan peta Karnaugh untuk X1 (A), X2 (A), X1 (B), X2 (B), X1 (C) dan X2 (C) masing-masing.
• Ekspresi yang diperkecil adalah sebagai berikut:

X1 SEBUAH = SEBUAH (11.8)
X2 A = A + BC (11.9)
X1 B = B (11.10)
X2 B = A + B + C (11.11)
X1 C = C (11.12)

X2 C = B + C (11.13)

• Figure 11.29
• Figure 11.31

  7. Problem [kembali] 

    

1. Perhatikan Gambar Rangkaian Bias Pembagi tegangan berikut. Hitunglah nilai tegangan emiter dan tegangan kolektor jika diketahui:
   
   
   
   
   Jawab:
   
   
   
2. Dalam rangkaian transistor pnp, arus kolektor adalah 10 mA. Jika 90% lubang yang dipancarkan mencapai kolektor, arus emitor adalah:
   Jawab:
   
   
   
3. Dalam penguat emitor umum, resistansi input dan output dari rangkaian adalah 400Ω dan 4kΩ. Jika penguatan transistor saat ini adalah 100, perolehan daya amplifier adalah:
    Jawab:
   
   Resistansi input   =  400Ω
   Resistansi output =  4kΩ
   Penguatan transistor (Betha) = 100
   
   Daya amplifier :
   
   

  8. Pilihan Ganda [kembali] 

    

1. Apa salah satu tugas penting yang dilakukan transistor?
   a. Menguatkan sinyal lemah
   b. Mengatur tegangan
   c. Meluruskan garis tegangan
   d. Memancarkan cahaya
   
   Jawab: a. Menguatkan sinyal lemah

2. Kebanyakan electron pada basis transistor npn mengalir
   a. Keluar dari ujung basis
   b. Menuju kolektor       
   c. Menuju emitor
   d. Menuju tegangan basis
   
   Jawab: b. Menuju kolektor

3. Siapa yang pertama kali menemukan sambungan transistor
   a. Bell
   b. Marconi
   c. Faraday
   d. Schockley
   
   Jawab: d. Shockley

  9. Link Download [kembali]

• Download rangkaian proteus 11.27 disini
• Download rangkaian proteus 11.29 disini
• Download rangkaian proteus 11.31 disini
• Download video rangkaian 11.27 disini
  
• Download video rangkaian 11.29 disini
• Download video rangkaian 11.31 disini
• Download sheet transistor disini
• Download sheet dioda disini
• Download HTML disini